
Abbildung 1: MEMS Sensor mit angepasstem Elektrodendesign, um spezielle mechanische Schwingungsmoden effizient anzuregen.
Einleitung und Motivation
Flüssigkeiten spielen eine zentrale Rolle in nahezu jedem Aspekt unseres Lebens von Körperflüssigkeiten über Lebensmittel bis hin zu chemischen Prozessen und technischen Anwendungen. Die Kenntnis über die physikalischen Eigenschaften von Flüssigkeiten wie Viskosität und Dichte erlaubt vielfältige Rückschlüsse auf deren aktuellen Zustand.
Um diese Eigenschaften zu bestimmen, ist eine bidirektionale Kraftübertragung zwischen einer mechanischen Struktur und der Flüssigkeit notwendig. Im Labor werden diese Eigenschaften oftmals mit großen Tischgeräten bestimmt, was eine ausreichend große Probenmenge der Flüssigkeit (typischerweise mindestens 50 ml) voraussetzt und auch keine direkte, im jeweiligen technischen System integrierte Überwachung der Flüssigkeit ermöglicht. Miniaturisierte Sensoren basierend auf der Technologie der mikro-elektromechanischen Systeme (MEMS) erlauben eine solche Vor-Ort-Integration der Messtechnik, sind aber bisher oftmals dadurch eingeschränkt, dass nur sehr geringe Kräfte auf die Flüssigkeit übertragen werden können und mechanische Bewegungen insbesondere in hochviskosen Flüssigkeiten sehr stark gedämpft werden.
Hier kommen an der TU Wien speziell für den Einsatz in Flüssigkeiten entwickelte MEMS-Sensoren ins Spiel. Die Mikrostrukturen bestehen aus schwingfähigen Siliziumplatten mit darauf integrieren piezoelektrischen Wandlern, welche in Resonanz betrieben werden. Durch eine spezielle Strukturierung der metallischen Kontaktelektroden können gezielt unkonventionelle, mechanische Schwingungsmoden resonant angeregt werden, die selbst in hochviskosen Flüssigkeiten nur eine sehr geringe Dämpfung und damit einen hohen Gütefaktor aufweisen. Der Gütefaktor Q, auch Q-Faktor genannt, ist ein Maß für die Dämpfung und wird als Messgröße herangezogen, da eine direkte Korrelation zwischen Viskosität, Dichte und Q besteht.
Herstellung von piezoelektrischen Resonatoren
Die an der TU Wien entwickelten Sensoren basieren auf Prozesstechnologien, die standardmäßig für die Fertigung von Silizium MEMS Bauelementen eingesetzt werden. Der Prozess startet mit einem sogenannten Silicon-on-insulator (SOI) Wafer mit 100 mm Durchmesser, der mit stresskompensierten Dünnfilmen aus Siliziumoxid und Siliziumnitrid beschichtet wurde. Eine Bodenelektrode wird durch Aufdampfen oder Sputterabscheidung aufgebracht und mit konventionellen Lithographie- und Ätzverfahren strukturiert. Anschließend wird die piezoelektrische Schicht aus Aluminiumnitrid (AlN) durch reaktives Sputtern von einem Aluminiumtarget in Stickstoffatmosphäre abgeschieden. Die Topelektrode wird dann ähnlich zur Bodenelektrode realisiert. Die letztlich schwingende Struktur wird durch deep reactive ion etching (DRIE) hergestellt, womit sich senkrechte Gräben in Silizium ätzen lassen. Um die nun bereits erkennbare Platte freizustellen, werden von der Rückseite mit DRIE Gräben durch den gesamten Wafer hindurch geätzt. Der DRIE-Prozess stoppt an der eingeschlossenen Oxidschicht im SOI Wafer, welche abschließend durch einen nasschemischen Prozess mit Hilfe von Flusssäure entfernt wird. Der Wafer wird zuletzt vereinzelt, die Sensoren in Keramikpackages eingebaut und mit Drahtbonds mit dem Package verbunden. Ein fertiger Sensor ist in Abb. 1 zu sehen.
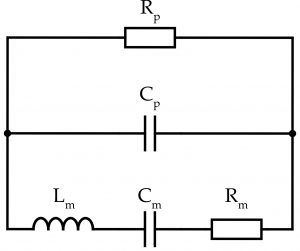
Abbildung 2: Butterworth-van-Dyke Ersatzschaltbild.
Messtechnik
Piezoelektrische Wandler sind grundsätzlich wie Plattenkondensatoren aufgebaut und können damit elektrisch durch ihre Kapazität und ihren Leckstrom beschrieben werden. MEMS Resonatoren mit piezoelektrischem Wandler werden daher häufig durch ein Butterworth-van-Dyke Ersatzschaltbild (siehe Abb. 2) beschrieben, wobei die Größen Cp und Rp die Wandlerkapazität und den elektrischen Widerstand der piezoelektrischen Schicht darstellen. Die mechanische Resonanz wird durch den LCR-Schwingkreis und damit durch die Größen Cm, Lm und Rm modelliert. Die Resonanzfrequenz wird dabei durch Cm und Lm beschrieben und die Dämpfung des Resonators durch Rm berücksichtigt. Wird der piezoelektrische Wandler elektrisch z.B. durch ein Sinussignal angeregt, so wird dadurch auch eine mechanische Schwingung der gleichen Frequenz ausgelöst. Da der Wandler bidirektional ist, erzeugt die mechanische Schwingung ihrerseits wiederum elektrische Ladungen, die zum Gesamtstrom durch das Bauelement beitragen. Wenn sich die Frequenz einer Resonanz annähert, nimmt die Amplitude der mechanischen Schwingung bei gleichbleibender Amplitude des anregenden Signals zu, wodurch mehr Ladungen generiert werden und somit ein höherer Strom fließt. Eine frequenzabhängige Messung der Impedanz Z weist also bei jeder mechanischen Resonanz ein Impedanzminimum auf bzw. ein Maximum in der Konduktanz G. Aufgrund dieser direkten Kopplung zwischen mechanischer und äquivalenter elektrischer Resonanz ist es möglich, das mechanische Verhalten des Resonators vollständig elektrisch zu charakterisieren und den mechanischen Q-Faktor durch Q=1⁄Rm √(Lm⁄Cm) zu bestimmen. Ein typisches Konduktanz- und Suszeptanzspektrum einer Resonanz ist in Abb. 3 zu sehen.
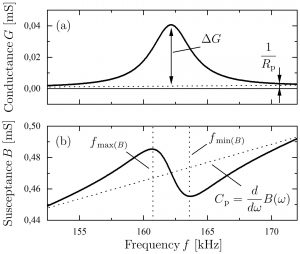
Abbildung 3: Typisches Konduktanz- (a) und Suszeptanzspektrum (b) einer mechanischen Resonanz.
Unkonventionelle Schwingungsmoden
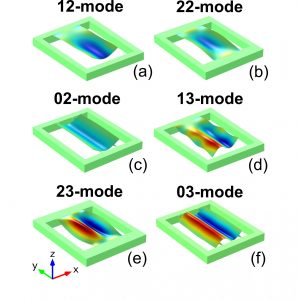
Abbildung 4: Finite Elemente Simulation der „roof tile shaped modes“ für unterschiedliche Modenordnungen sowie unterschiedliche
Aufhängungsdesigns. Blau markiert sind Bereiche die gestaucht werden und rot solche, die gedehnt werden.
Wie bereits oben erwähnt werden mechanische Bewegungen in Flüssigkeiten mit zunehmender Viskosität und Dichte sehr stark gedämpft (diesen Effekt kennt jeder, der in einem Schwimmbecken versucht, durch das Wasser zu gehen). Dies stellt ein enormes Problem für Mikrostrukturen da, die auf Grund der geringen Größe nur geringe Kräfte erzeugt werden können. Vor einigen Jahren wurden jedoch am Institut für Sensor- und Aktuatorsysteme der TU Wien spezielle, unkonventionelle Schwingungsmoden in mikroskopischen Balkenstrukturen gefunden, die selbst in hochviskosen Flüssigkeiten nur schwach gedämpft werden. In Abb. 4 sind Finite-Elemente Simulationen von einigen Ordnungen dieser mechanischen Moden zu sehen, die auf Grund ihrer Ähnlichkeit zu Dachziegeln als roof-tile-shaped modes („Wellpappen-Moden“) bezeichnet werden. Die spezielle Form dieser Moden erfordert eine an jede Mode angepasste Elektrodengeometrie, um einen Ausgleich von Oberflächenladungen unterschiedlichen Vorzeichens unter der gleichen Elektrode zu vermeiden. Durch diese geschickte Designwahl kann die Höhe des Konduktanzmaximums und damit auch das Signal-zu-Rauschen Verhältnis um 1-2 Größenordnungen erhöht werden, ohne in zusätzliche Maßnahmen, wie z.B. in einen spezifischen Regelkreis, investieren zu müssen [1].
Viskositätsmessung in Bitumen
Eine Anwendung dieser unkonventionellen Schwingungsmoden demonstriert beeindruckend deren herausragenden Eigenschaften. So ist es möglich, mit den an der TU Wien entwickelten piezoelektrischen MEMS Resonatoren bei erhöhten Temperaturen von >70°C die Viskosität von bituminösen Materialien bis zu einer dynamischen Viskosität von 64000 mPa∙s zu messen. Die Resonatoren werden dazu bei Frequenzen um die 3,5 MHz betrieben. Die Ergebnisse dieser Messung sind in Abb. 5 dargestellt und demonstrieren eine gute Übereinstimmung zwischen MEMS Sensor und einem handelsüblichen Brookfield DV3T Viskosimeter als Referenz [2].
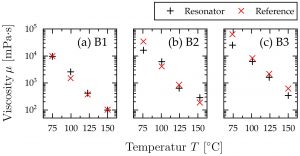
Abbildung 5: Gemessene Viskosität verschiedener Bitumenproben in Abhängigkeit der Temperatur. Die Messung wurde sowohl mit dem an der TU Wien entwickelten MEMS Sensor als auch mit einem handelsüblichen Brookfield DV3T Viskosimeter als Referenz durchgeführt.
Partikeldetektion in Schmierölen

Abbildung 6: An der TU Wien entwickelter piezoelektrischer MEMS Sensor zur Detektion von „varnish“-Partikeln in Schmierölen.
Während der Q Faktor ein Maß für die Dämpfung eines Resonators in Flüssigkeiten ist, so ist die Resonanzfrequenz ein Maß für die effektive Masse des Resonators. Lagern sich in der Flüssigkeit also Partikel am Resonator an, so führt dies zu einer Verschiebung der Resonanzfrequenz, welche in erster Näherung proportional zur Massenzunahme ist. Den Ansatz, auf diese Weise mikroskopische Waagen in Luft oder in Vakuum zu realisieren, gibt es schon seit Jahrzehnten, allerdings ermöglichen die hohen Q-Faktoren, der unkonventionellen Schwingungsmoden nun eine rein elektrische Partikeldetektion direkt auch in hochviskosen Flüssigkeiten. Durch die Integration eines magnetischen Aktuators können magnetische Abriebpartikel zum Resonator transportiert werden, die sich dann auf dessen Oberfläche anlagern. Damit können diese Abriebpartikel in Schmierölen direkt im Ölkreislauf detektiert werden. Weiterhin bilden sich in Ölen rein durch Alterung ungewünschte, dielektrische Partikel (sogenannter varnish), welche durch einen integrierten dielektrophoretischen Aktuator angelagert und damit detektiert werden können. Um Querempfindlichkeiten zu minimieren, werden diese Sensoren immer differentiell zusammen mit einem Referenzsensor betrieben [3]. Ein Bild eines solchen Sensors ist in Abb. 6 dargestellt.
Zusammenfassung
Piezoelektrische MEMS Sensoren basierend auf einer Klasse unkonventioneller Schwingungsmoden wurden entwickelt, die selbst in hochviskösen Flüssigkeiten noch eine Messung von Viskosität und Dichte ermöglichen. Die Sensoren werden dabei rein elektrisch angeregt und ausgelesen. Durch die Integration von zusätzlichen Aktoren kann die Anwendungsbandbreite weiter erhöht werden, so ist es z.B. möglich gezielt Partikel anzulagern und deren Masse auf Grund des hohen Q-Faktors präzise zu bestimmen. Diese Sensortechnologie sollte daher als Plattform betrachtet werden, die eine Vielzahl von zukünftigen Anwendungen für MEMS Resonatoren in Flüssigkeiten eröffnet. Als weiterführende Literatur sei an dieser Stelle noch auf einen Übersichtsartikel in e&i verwiesen [4].
Referenzen
[1] G. Pfusterschmied, M. Kucera, W. Steindl, T. Manzaneque, V. Ruiz Díez, A. Bittner, M. Schneider, J. L. Sánchez-Rojas and U. Schmid, „Roof tile-shaped modes in quasi free-free supported piezoelectric microplate resonators in high viscous fluids“, Sensors and Actuators, B: Chemical, 237, pp. 999-1006 (2016).
[2] G. Pfusterschmied, C. Weinmann, M. Hospodka, B. Hofko, M. Schneider and U. Schmid, „Sensing fluid properties of super high viscous liquids using non-conventional vibration modes in piezoelectrically excited MEMS resonators“ Proc. of Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems (MEMS) (2019), pp. 735-738.
[3] F. Patocka, C. Schneidhofer, N. Dörr, M. Schneider and U. Schmid, „Novel resonant MEMS sensor for the detection of particles with dielectric properties in aged lubricating oils“, Sensors and Actuators A: Physical, pp. 112290 (2020).
[4] M. Schneider, G. Pfusterschmied, F. Patocka and U. Schmid, „High performance piezoelectric AlN MEMS resonators for precise sensing in liquids“, e & i Elektrotechnik und Informationstechnik, 137, pp. 121-127 (2020).
Acknowledgments
This work was partially supported by the Austrian Research Promotion Agency within the „Austrian COMET-Program” in the frame of K2 XTribology (project no. 824187 and 849109). This financial support is gratefully acknowledged.
Autoren:
Michael Schneider
Georg Pfusterschmied
Florian Patocka
Ulrich Schmid
michael.schneider@tuwien.ac.at
+43 1 58801 76636


